Proporção áurea? Você já ouviu falar neste termo? Ou no número de ouro? Quem sabe no retângulo de ouro, ou ainda razão áurea?
A proporção áurea e o número de ouro são dois elementos inter-relacionados, porém, são dois elementos distintos.
Estes elementos foram desenvolvidos ao longo de vários séculos, à medida que os conceitos matemáticos foram se desenvolvendo.
Ao lado da questão matemática surgia uma relação entre proporções de figuras geométricas que se dizia ser a forma mais harmônica para se utilizar. Ficou conhecida como proporção áurea, criando um debate quase religioso entre os que aceitam e os que não toleram a ideia.
O fato é que a proporção áurea segue viva a séculos, admirada e odiada.
O que é o número de ouro
O número de ouro é o resultado que se obtém após dividir uma reta em duas partes não iguais, e, ao efetuar o quociente entre a reta inteira e seu maior segmento, encontramos o número irracional 1,6180339887…
Veja a representação abaixo:
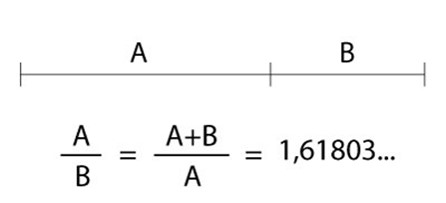
Figura 1 – Reta com Proporção Áurea
A reta que originou este número foi obtida em relações geométricas efetuadas no pentagrama regular, símbolo dos seguidores da escola de Pitágoras. Este pentagrama é facilmente reconhecido quando tem inscrito a estrela de cinco pontas, formada pelas diagonais da figura.
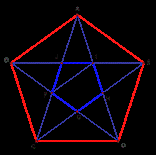
Figura 2 – Pentagrama Regular
O número de ouro é conhecido como “Phi” em homenagem ao escultor e arquiteto grego Phídeas (470 – 425 a.C.). O número é representado pela letra grega Φ.
Embora o número tenha sido batizado com referência a Phídeas, a relação foi apresentada pelo matemático Euclides de Alexandria, que viveu no século III aC, quando formulou a teoria da média e extrema razão.
É bom lembrar que Euclides na sua famosa obra Os Elementos, organizou o conhecimento sobre matemática e geometria da época, portanto muito do que ele catalogou já existia bem antes daqueles anos.
O retângulo de ouro e a proporção áurea
O retângulo de ouro é aquele em que a divisão de seu lado maior pelo lado menor resulta no número de ouro, como na figura abaixo.
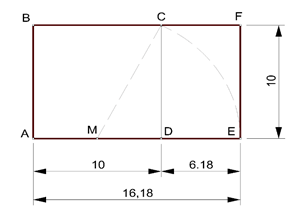
Figura 3- Retângulo de Ouro
Ele é reconhecido por outros nomes como retângulo áureo e esta proporção é definida como Proporção Áurea.
Então se você quer obter um retângulo com a proporção áurea, conhecendo um dos lados, é somente fazer a relação matemática que leve ao número de ouro. Se tiver o lado menor multiplique por Φ e caso tenha o lado maior, divida-o por Φ. Simples assim.
O Número de Ouro, a proporção áurea e a Sequência Fibonacci
A descoberta do número de ouro e suas primeiras aplicações ocorreram no século 3 a.C., mas o número continuou exercendo seu fascínio nos estudiosos do tema.
Já no século 13 d.C. Leonardo Fibonacci, propôs um problema sobre multiplicação de coelhos que geravam uma sequência de números, que se denominou Sequência de Fibonacci.
O problema diz que um homem pôs um par de coelhos em um local cercado. Pergunta-se: quantos pares de coelhos podem ser gerados a partir deste par em um ano se, supostamente, todos os meses, cada par dá à luz um novo par, que se torna fértil a partir do segundo mês?
Graficamente é o que se mostra na figura seguinte:
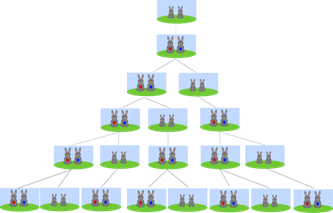
Figura 4 – Sequência Fibonacci com o Problema dos Coelhos
Pode se definir a sequência de Fibonacci como uma sequência de números inteiros, começando por 0 ou 1, na qual cada termo subsequente corresponde à soma dos dois anteriores. O resultado: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 521…
Mas o que tem a ver esta sequência com o número de ouro? Esta é a relação que torna estes números algo mágico, intrigando a tanto tempo os estudiosos. Quando se divide o número seguinte pelo anterior, o resultado vai se aproximando gradativamente do número de ouro.
E o mais intrigante, quando se faz um arranjo geométrico representando estes números como quadrados, os resultados vão gerando retângulos que se aproximam cada vez mais de retângulos com a proporção áurea.
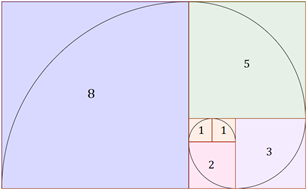
Figura 5- Fibonacci e o Retângulo de Ouro
Feitos os quadrados, traçamos uma espiral a partir da origem dos quadrados, fazendo com que seus arcos concêntricos passem pelos pontos das sucessivas divisões entre os quadrados.
A espiral que se obtém é definida como espiral de ouro e sua forma pode ser encontrada em muitos elementos da natureza, segundo os defensores da teoria, como a concha do Nautilus Marinho.

Figura 6 – Concha Nautilus Marinho
Aplicações e Mitos da proporção áurea nas construções
A proporção áurea tem, segundo os admiradores desta teoria, o que se considera como as proporções mais agradáveis ao olho humano, por isto seu uso passou a ser utilizado com grande intensidade como parâmetro para as artes, arquitetura e construções.
Todavia o manto de divindade que se associou a teoria, como explicação simplificada para coisas da natureza e do próprio corpo humano acabaram por emprestar a proporção áurea requintes de fanatismo, servindo de explicação ao que ela, de fato, não explica.
Muitas situações em que se diz que a proporção foi utilizada são mitos ou obra de admiradores extremados da teoria que gostariam de vê-la em mais aplicações do que realmente é possível relacionar.
Da mesma forma que existem admiradores da teoria há também os que querem provar que ela não é o que se diz, como, é claro, em toda grande teoria que se preze.
Há relatos que a proporção áurea foi utilizada desde as construções das pirâmides do Egito, passando por construções gregas como o Parthenon e obras de Leonardo da Vinci.
Já na história moderna, onde podemos relacionar os fatos de forma mais confiável temos exemplos nas obras do arquiteto suíço, naturalizado francês, Le Corbusier (1887-1965).
Construções relacionadas com a proporção áurea
Vamos ver na sequência algumas construções, nas quais se diz ter havido o uso das proporções áurea. Frisando que digo “que se diz” porque muitas delas foram construídas antes da formalização desta teoria.
Parthenon na Grécia:

Figura 7 – Parthenon do arquiteto Phideas
Catedral de Notre Dame:
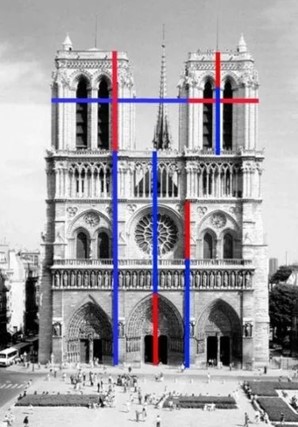
Figura 8 – Catedral de Notre Dame
Taj Mahal:

Figura 9 – Taj Mahal
Torre Eiffel:

Figura 10 – Torre Eiffel
Conclusões sobre o uso da proporção áurea nas construções
Revendo o texto podemos ver que o uso do número de ouro para determinar uma proporção ideal tem uma base mais romântica do que funcional, sem menosprezar sua importância.
É uma relação matemática interessante, sob contexto da história, porém não guarda por si só uma verdade absoluta como proporção ideal.
Na pesquisa para produção deste post encontramos artigos que assumem como certas informações que não tem como ser sustentadas, senão por pura crença.
Matemática e geometria são alguns dos pilares do desenvolvimento da civilização moderna e a proporção áurea é uma das descobertas feitas no caminho desta evolução, que certamente contribuiu para melhorar as técnicas já utilizadas e, também, as que foram criadas.
Acompanhe os artigos publicados aqui em nosso Blog Gerência de Obras e aproveite para deixar seu comentário contribuindo com o tema analisado.
Perguntas sobre o tema:
Para que serve a proporção áurea?
A proporção áurea é uma relação geométrica entre dois lados de um retângulo, cuja razão entre o maior lado e o menor resulta no número 1,618, que é tido como o número de ouro. Diz se que a figura com estas proporções tem mais harmonia aos olhos humanos.
Como utilizar a proporção áurea?
Se você quer encontrar a altura de um retângulo com a proporção áurea e já possui o valor da base, divida este número por 1,618. Caso tenha a altura e queira encontrar a base, multiplique o valor por 1,618 que é o número de ouro.
Como surgiu o número de ouro?
O número de ouro é uma razão matemática obtida quando se divide um segmento de reta em duas partes desiguais, sendo o resultado da divisão do maior segmento pelo menor igual a divisão da reta inteira pelo maior segmento. Seu registro oficial vem dos trabalhos do matemático Euclides, século III a.C., mas sua formulação acompanhou o desenvolvimento da própria matemática e geometria, quando definiu os números comensuráveis e incomensuráveis. É um número irracional, comumente aproximado por 1,618.
Engenheiro Civil e Técnico de Edificações, formado pela Universidade Católica de Goiás em 1996. Ao longo dos anos tive a oportunidade de trabalhar no planejamento, execução e controle de obras de construção civil residenciais, comerciais e institucionais, de pequeno a grande porte. No site Gerência de Obras compartilho informações e experiências adquiridas com quem pretende construir ou reformar.